Szybki start
Optymalizacja bez ograniczeń
| Funkcja celu: | 0,1x4 - 10x2 - 20x + y2 |
1. Wybór optymalizacji bez ograniczeń i wprowadzenie
funkcji celu.
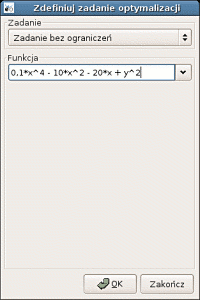
2. Wybór metody Marquardta oraz zadanie punktu startowego.
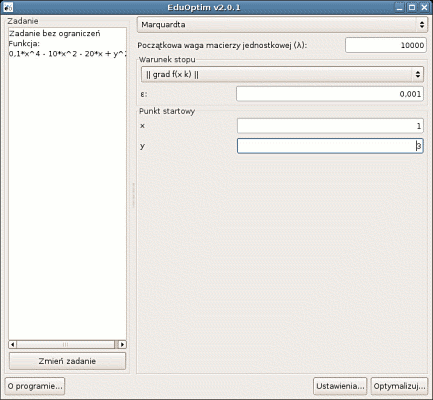
3. Szczegółowy opis poszczególnych kroków optymalizacji.
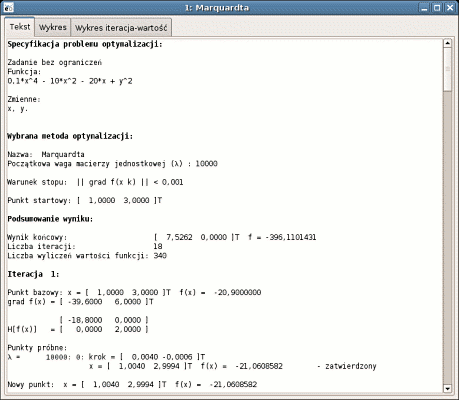
4. Przebieg optymalizacji przedstawiony na wykresie.
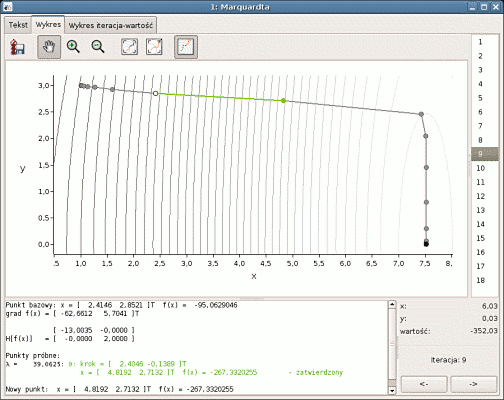
Optymalizacja z ograniczeniami
Optymalizacja zadanej funkcji celu przy obszarze dopuszczalnym będącym lewą połówką koła o środku w punkcie (0; 0) i promieniu 4 jednostki.| Funkcja celu: | 0,1x4 - 5x2 - 10x + y2 |
| Ograniczenia: | |
| x ≤ 0 |
1. Wybór optymalizacji z ograniczeniami
i wprowadzenie funkcji celu.
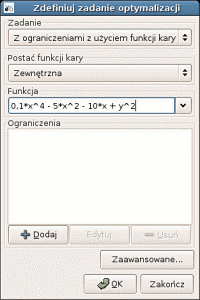
2. Wprowadzanie ograniczenia (koło o promieniu 4
i środku w punkcie (0,0)).
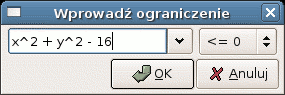
3. Wprowadzone zadanie optymalizacji wraz
z ograniczeniami.
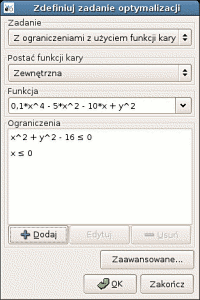
4. Wybór metody Hooke'a-Jeevesa oraz punktu startowego.
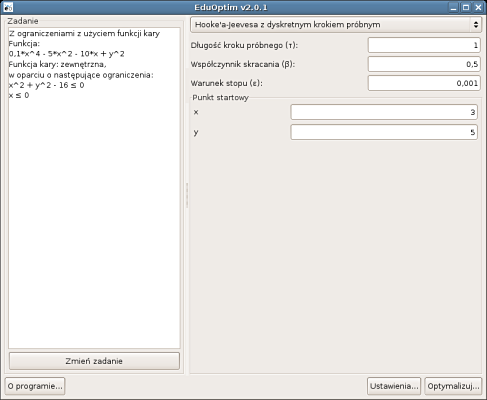
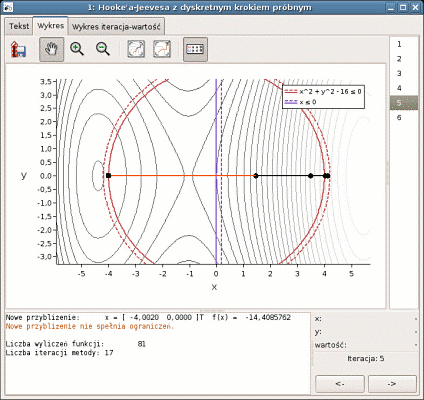
5. Kolejne przybliżenia wyniku przedstawione na wykresie
(obszar dopuszczalny to lewa część koła).