Quick Start
Unconstrained Optimization
| Objective function: | 0.1x4 - 10x2 - 20x + y2 |
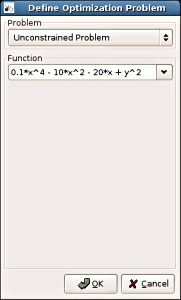
1. Choosing unconstrained optimization problem and entering
the objective function.
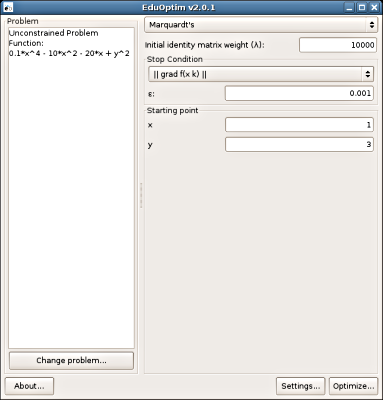
2. Choosing Marquardt's method and entering coordinates of
the starting point.
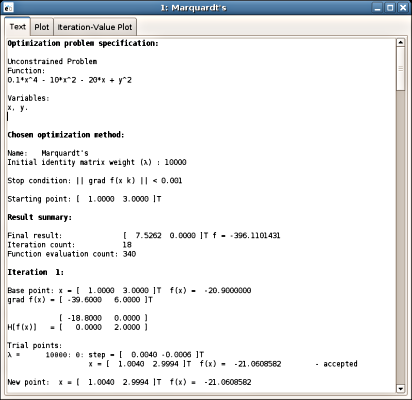
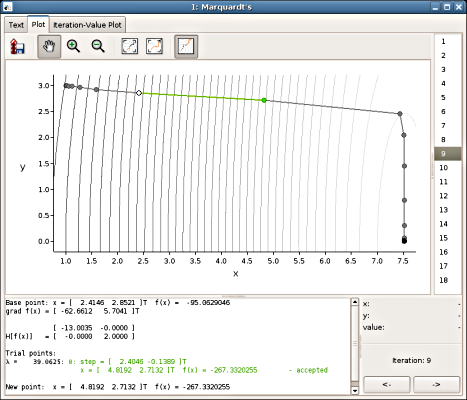
3. Detailed description of each optimization step.
4. Optimization process illustrated over a function
plot.
Constrained Optimizaton
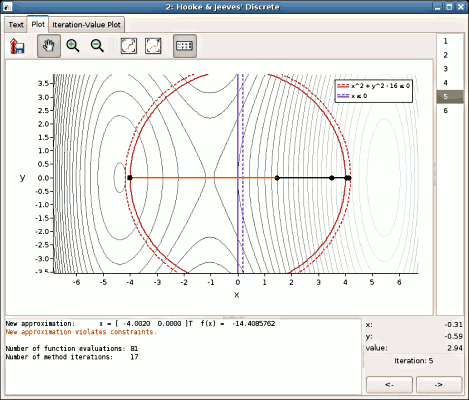
Optimization of a function with feasible region being the left half of a circle with origin in point (0; 0) and 4 unit radius.
| Objective function: | 0.1x4 - 5x2 - 10x + y2 |
| Constraints: | |
| x ≤ 0 |
1. Choosing constrained optimization problem and entering the
objective function.
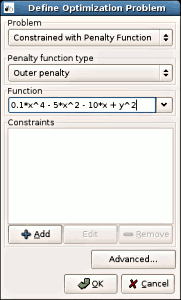
2. Entering constraint (circle with 4 unit radius and origin
in the point (0; 0)).
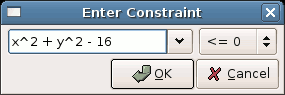
3. The entered optimization problem with constraints.
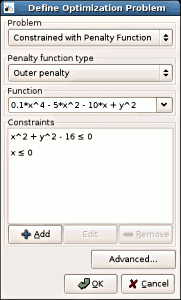
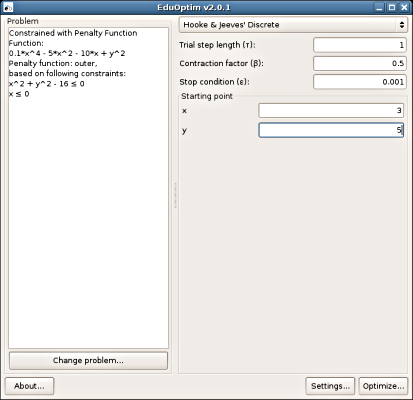
4. Choosing Hooke-Jeeve's method and entering coordinates of
the starting point.
5. Subsequent approximations of the result shown on a plot
(the feasible region is the left half of the circle).