Dokumentacja klasy SteepestDescent

#include <SteepestDescent.h>

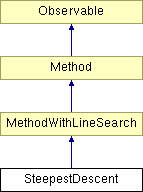
Diagram dziedziczenia dla SteepestDescent

Lista wszystkich składowych.

Opis szczegółowy

Metoda największego spadku (Cauchy'ego).

Gradientowa metoda kierunków poprawy.

Podstawą teoretyczną metody są dwa twierdzenia:

1. Jeśli istnieje taki kierunek 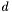$d$ , że

$(\nabla f(x))^T d < 0 ,$

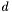to $d$ jest kierunkiem poprawy:

$f(x + \tau d) < f(x) ,$

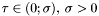gdzie $\tau \in (0; \sigma), \: \sigma > 0$ .

2. Dla liniowego modelu funkcji - rozwinięcia w szereg Taylora pierwszego rzędu:

$f(x + \tau d) = f(x) + \tau d^T f'(x) + O(\tau^2) ,$

spośród wszystkich kierunków spełniających warunek z twierdzenia 1, kierunkiem najszybszego spadku jest

$d = -\nabla f(x) .$

Informacje wejściowe:
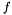$f$ - minimalizowana funkcja 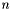$n$ zmiennych,
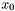$x_0$ - dowolnie wybrany punkt startowy,
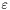$\varepsilon$ - dokładność warunku stopu,
warunek stopu - do wyboru:

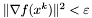
$\|\nabla f(x^k)\|^2 < \varepsilon$
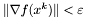
$\|\nabla f(x^k)\| < \varepsilon$
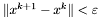$\|x^{k+1} - x^k\| < \varepsilon$ ,
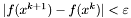$|f(x^{k+1}) - f(x^k)| < \varepsilon$ ,
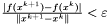$\frac{|f(x^{k+1}) - f(x^k)|}{\|x^{k+1} - x^k\|} < \varepsilon$ ,

wybrana metoda minimalizacji w kierunku wraz z parametrami.

Oznaczenia:
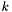$k$ - numer aktualnej iteracji,
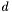$d$ - aktualny kierunek poszukiwań,
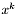$x^k$ - aktualny punkt próbny,
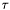$\tau$ - długość wykonywanego aktualnie kroku.

Procedura.

Krok wstępny:
Podstawiamy:

$x^1 = x^0 ,$

$k = 1 .$

Krok 1:
Wyznaczamy kierunek przeciwny do gradientu:

$d = -\nabla f(x^k) .$

Krok 2:
Sprawdzamy warunek stopu:
Jeśli 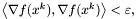$\left<\nabla f(x^k), \nabla f(x^k)\right> < \varepsilon ,$ to STOP. W przeciwnym wypadku przechodzimy do kroku 3.

Krok 3:
Wykonujemy krok w kierunku 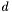$d$ o optymalnej długości $\tau$ :

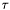$\tau = \arg \min_{\tau} f(x^k + \tau d) ,$

$x^{k+1} = x^k + \tau d .$

Podstawiamy 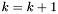$ k = k + 1 $ i przechodzimy do kroku 1.

Uwagi.
Metoda opiera się na liniowym modelu funkcji (patrz twierdzenie 2) i dla funkcji wyższego rzędu jest najczęściej wolno zbieżna. Podstawową wadą, wpływającą na wolną zbieżność, jest "zygzakowaty" charakter przebiegów optymalizacji. Dokładne metody minimalizacji w kierunku (a taka jest tu wykorzystywana w kroku 3) zatrzymują się w punkcie, w którym gradient funkcji 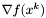$\nabla f(x^k)$ jest prostopadły do aktualnego kierunku poszukiwań 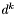$d^k$ . Kolejny kierunek 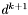$d^{k+1}$ będzie, zgodnie z podstawowym założeniem metody, równoległy do gradientu. W ten sposób metoda w całym swym przebiegu operuje tylko dwoma prostopadłymi do siebie kierunkami, silnie zależnymi od punktu początkowego.

Metoda zaimplementowana na podstawie opisu zamieszczonego w:
Findeisen W., Szymanowski J., Wierzbicki A.: Teoria i metody obliczeniowe optymalizacji. Warszawa, PWN 1977.

Niniejszy dokument został półautomatycznie wycięty z dokumentacji kodu źródłowego programu Eduoptim 2. Pełna dokumentacja dostępna jest wraz ze źródłami bądź osobno w dziale pliki.
Hierarchia klas w programie nie odpowiada klasyfikacji metod optymalizacji.